Le théorème présenté est un joli résultat liant les matrices stochastiques et les groupes, en passant par les valeurs propres et les nombres complexes de module 1 (ce qui en fait un beau développement pour l’agrégation de mathématiques !). Il existe différentes versions du théorème de Perron-Frobenius, selon les hypothèses sur la matrice. Celle présentée nous donne des informations sur le spectre des matrices stochastiques irréductibles. Plus précisément, on montre le théorème suivant :

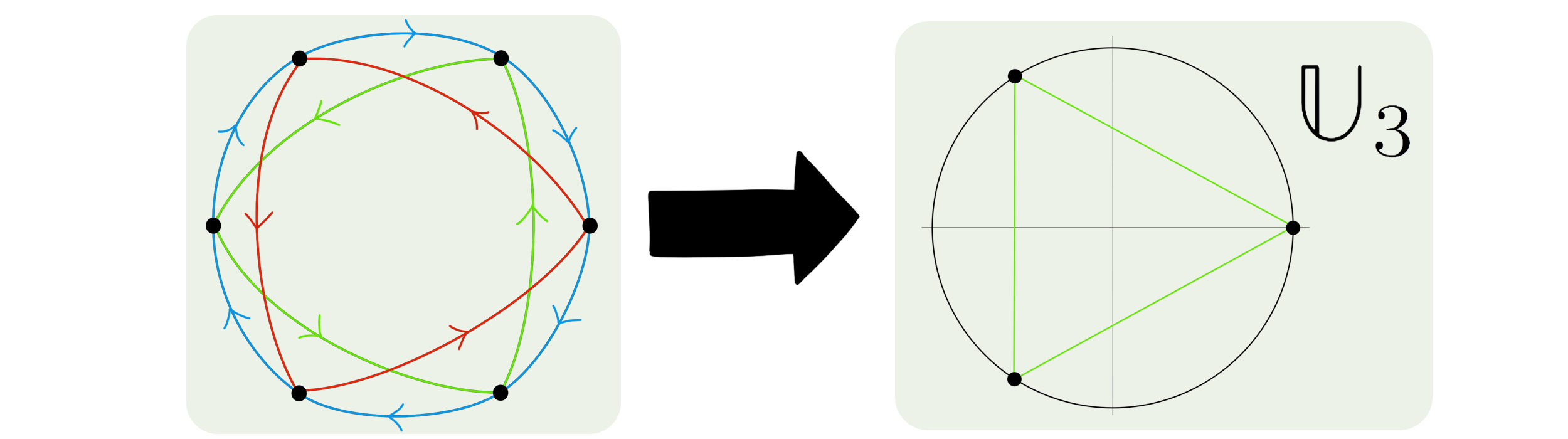
Théorème : Soit $A \in \mathcal M_n(\mathbb R)$ une matrice stochastique et irréductible. Alors le rayon spectral de $A$ est 1, et l’ensemble des valeurs propres (complexes) de $A$ de module 1 forme un sous-groupe de $(\mathbb S^1, .)$.

On montre même plus précisément, pour $\lambda$ et $\mu$ deux valeurs propres de module 1 de vecteurs propres respectifs $X$ et $Y$; que le vecteur $X.Y := (X_k.Y_k)_k$ est un vecteur propre pour $\lambda.\mu$ !

La preuve du théorème est disponible ici.

Références :

• Serge Francinou, Hervé Gianella et Serge Nicolas. Oraux X-ENS, Algèbre 2. Pages 83-85.
• Denis Serre. Les Matrices, Théorie et pratique. 2001