Mon stage de fin de M1 portait sur des processus de branchement en temps discret. Le mémoire de stage est disponible ici.
Il a été réalisé à l’Université du Québec à Montréal, sous la direction d’Hélène Guérin et de Félix Foutel-Rodier.
Les processus étudiés pendant le stage sont des modèles probabilistes, qui peuvent permettre par exemple de décrire l’évolution d’une population, ou bien la propagation d’une épidémie. Le modèle le plus classique est celui des processus de Galton-Watson, introduit au 19e siècle, qui ont été étudiés dans la première partie du stage. La construction d’un espace de probabilité d’arbres aléatoires apparaît au 20e siècle, parfois due à Neveu, parfois à Ulam et Harris, et permet de mieux comprendre certains résultats sur ces processus. En particulier, le Théorème de Kesten et Stigum se montre à l’aide d’une technique de décomposition épinale. Cette méthode, présentée initialement par Lyons, Pemantle et Peres dans l’article [RLP95] a l’avantage de se généraliser à des modèles plus complexes, comme ceux étudiés dans la fin du stage : les processus de Crump-Mode-Jagers. Ce modèle est plus réaliste que celui de Galton-Watson, mais plus complexe à étudier.
Processus de Galton-Watson
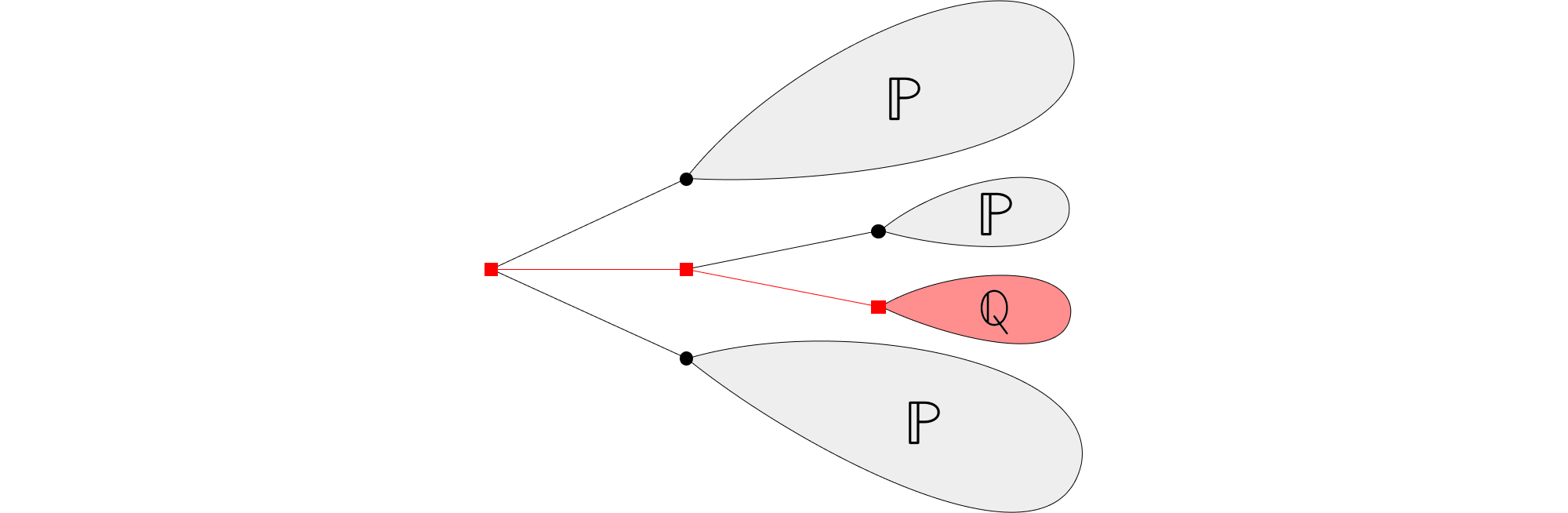
Partons d’un groupe d’individus, et imaginons qu’ils donnent naissance indépendamment les uns des autres à un nombre aléatoire d’enfants, suivant la même mesure de probabilité $P$, puis meurent. Appelons ces individus la génération 0, et leurs enfants la génération 1. On peut recommencer le processus pour chaque individu de la génération 1, et obtenir la génération 2, et ainsi de suite. Les processus de Galton-Watson modélisent ce genre de situation. C’est-à-dire que les générations sont séparées, les individus ne se reproduisent pas entre eux, mais donnent naissance tous seuls à des enfants (on parle de reproduction asexuée), et ce une seule fois dans leur vie. Un outil utile pour visualiser l’évolution d’un tel processus est un arbre aléatoire. Ici, la génération 0 est représentée en noir, la première en rouge et la seconde en bleu.
Processus de Crump-Mode-Jaggers (CMJ)
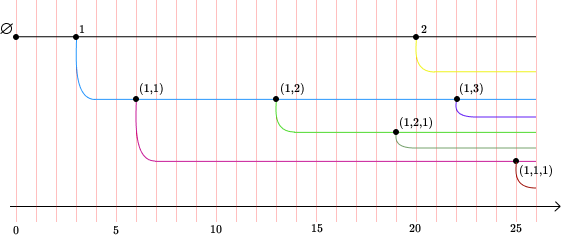
Les processus CMJ sont plus complexes. Dans ce modèle, les individus donnent naissance au cours de leur vie à plusieurs enfants, à des dates précises. Ceci change l’échelle de temps, qui compte plutôt les années que les générations, car ces dernières peuvent désormais se superposer. Ci-dessous, on a représenté un exemple d’évolution d’une population selon ce modèle. Chaque ligne colorée représente la vie d’un individu, et chaque individu est noté par un point. L’axe des abcisses représente le temps.
[RLP95] Robin Pemantle, Russell Lyons and Yuval Peres. Conceptual proofs of LlogL criteria for mean behaviour of branching processes. The Annals of Probability, 23(3) :1125 – 1138, 1995.