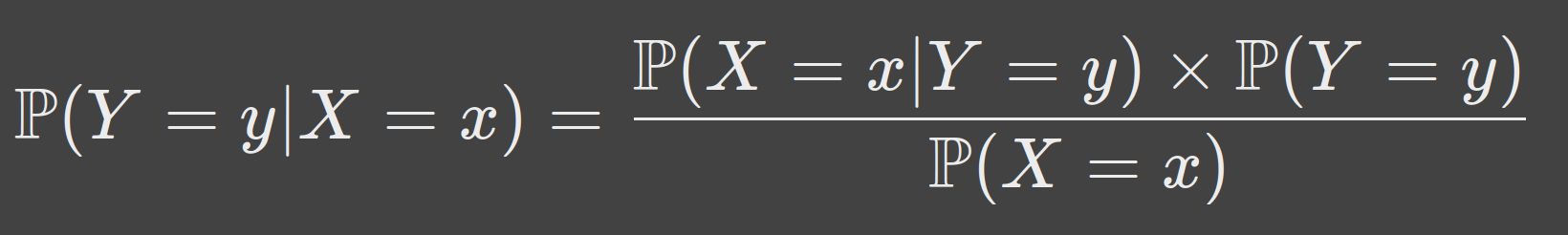Dans le cadre du TP autour de la prédiction du trafic de la ville de Rennes, le modèle ‘Naive Bayes’ est utilisé. On détaille ici un peu plus la théorie derrière la pratique.
Reprenons l’exemple de l’état du trafic. Pour simplifier, on suppose qu’on a 2 entrées : nom_de_la_route et heure; et une sortie : etat_trafic. Les différentes valeurs possibles pour etat_trafic sont :
circulation_impossibletres_ralentiralentifluide
Pour résumer, le modèle Naïve Bayes essaye d’estimer, pour une entrée $x = $(nom_de_la_route, heure) la probabilité que la sortie soit chacune des 4 possibilités. Il retourne ensuite la valeur pour laquelle il a estimé la plus grande probabilité.
De manière plus précise, on modélise notre problème par un couple $(X, Y)$ de variables aléatoires vérifiant :
- $X$ est à valeur dans $\mathcal X = \mathcal D\times \mathcal H$, où $\mathcal D$ est l’ensemble des noms de route possibles et $\mathcal H$ l’ensemble des heures ({0, 1, …, 23}),
- $Y$ est à valeur dans $\mathcal Y$, l’ensemble des valeurs possibles du trafic. On encode pour la suite ces valeurs en $1, 2, 3$ et $4$.
Le modèle fonctionne de la manière suivante. Pour $x \in \mathcal X$, le modèle estime (à un facteur près) :
- $p_1$$ = \mathbb{P} (Y = 1 | X = x)$,
- $p_2$$ = \mathbb{P} (Y = 2 | X = x)$,
- $p_3$$ = \mathbb{P} (Y = 3 | X = x)$,
- $p_4$$ = \mathbb{P} (Y = 4 | X = x)$.
Puis il regarde laquelle de ces $4$ estimations est la plus grande, et retourne le choix corespondant.
C’est la manière dont le modèle estime les paramètres qui lui donne son nom (Naïve Bayes). Elle est basée sur le théorème de Bayes, et est dite ‘Naïve’ car elle fait une hypothèse assez forte sur $X$ (on explique pourquoi on fait cette hypothèse à la fin).
‘Naïve’ ?
Pour estimer les probabilités ci-dessus, le modèle fait l’hypothèse que les marginales de $X$ sont indépendantes conditionnellement à $Y$. C’est-à-dire, (si on note $X^{(1)}$ le nom de la route et $X^{(2)}$ l’heure) que pour tout nom de route $x^{(1)} \in \mathcal D$ , toute heure $x^{(2)} \in \mathcal H$ et toute valeur $y \in \mathcal Y$ de l’état du trafic, on a : $$ \mathbb P(X^{(1)} = x^{(1)}, X^{(2)} = x^{(2)} | Y = y) = \mathbb P(X^{(1)} = x^{(1)}| Y = y)\times \mathbb P( X^{(2)} = x^{(2)} | Y = y). $$
On rappelle que par définition, la probabilité que $X^{(1)} = x^{(1)}$ sachant que $Y=y$ est : $$ \mathbb P(X^{(1)} = x^{(1)}| Y = y) = \frac{\mathbb P(X^{(1)} = x^{(1)}, Y = y)}{\mathbb P(Y = y)} $$
Intuitivement, dire que $X^{(1)}$ et $X^{(2)}$ sont indépendantes conditionnellement à $Y$ peut être expliqué de la manière suivante. Imaginons que vous jouez avec une amie. Elle observe l’état du trafic sur une route, à une heure précise. Elle vous dit quel est l’état de la circulation, mais pas le nom de la route, ni l’heure. Vous devez alors deviner (au hasard) ces deux informations. Alors dans cette configuration, dire que $X^{(1)}$ et $X^{(2)}$ sont indépendantes conditionnellement à $Y$ c’est dire que le fait de connaître (en plus de l’état du trafic) le nom de la route n’influence pas votre supposition sur l’heure (ou de manière équivalente que connaître l’heure n’influence pas votre supposition sur le nom de la route).
Cette hypothèse est souvent très forte (d’où la dénomination ’naïve’), même si elle ne semble pas l’être dans cet exemple précis.
‘Bayes’ ?
Le théorème de Bayes fait le lien entre $\mathbb P (Y = y | X = x)$ et $\mathbb P (X = x | Y = y)$. Voici ce théorème : $$ \mathbb P (Y = y | X = x) = \frac{\mathbb P (X = x | Y = y)\times \mathbb P(Y = y)}{\mathbb P(X = x)} $$ Il permet ici, si on fait l’hypothèse d’indépendance des marginales conditionnellement à $Y$, d’estimer les probabilités $p_1, p_2, p_3, p_4$.
Estimer les probabilités ?
Pour estimer les 4 probabilités $p_1, p_2, p_3, p_4$, une première approche peut être la suivante. Par définition de la probabilité conditionnelle : $$ \mathbb p_1 = \mathbb P(Y = 1 | X = x) = \frac{\mathbb P(Y = 1, X = x)}{\mathbb P(X = x)}. $$ Si on dispose de $n$ données d’entraînement $(x_1, y_1), …, (x_n, y_n)$ (c’est-à-dire un tableau de données comme dans l’exercice !). On note $N_1(n)$ le nombre de fois où on observe $(x, 1)$ dans ces données, on peut alors approcher $\mathbb P(Y = 1, X = x)$ (grâce à la loi des grands nombres) par $\frac{N_1(n)}{n}$. Il est inutile d’avoir une approximation du dénominateur, $\mathbb P(X = x)$, car il va apparaître dans chacune des $4$ probabilités $p_1, p_2, p_3, p_4$ : on peut se contenter de choisir l’état $i$ du trafic pour lequel la probabilité $\mathbb P(Y = i, X = x)$ est la plus grande (ça sera la même que celle pour laquelle $p_i$ est la plus grande). Le potentiel problème de cette première approche est le suivant: si on a beaucoup de paramètres en entrées (c’est-à-dire si $X$ est à valeur dans un espace avec un grand nombre de dimensions), le nombre $N_1(n)$ de fois où on a observé l’entrée $x$ et la sortie $1$ risque d’être trop petit pour fournir une bonne approximation de $\mathbb P(Y = 1, X = x)$ (ou alors il faudrait un nombre $n$ de données d’entraînement beaucoup trop grand).
C’est pour palier à ce problème qu’on fait l’hypothèse ’naïve’ d’indépendance conditionnelle. Dans ce cas, l’approximation de $p_1$ se simplifie. Par le théorème de Bayes : $$ p_1 = \mathbb P(X = x| Y = 1) \times \frac{\mathbb P(Y = 1)}{\mathbb P(X = x)}. $$ Par l’hypothèse d’indépendance conditionnelle : $$ \mathbb P(X = x | Y = 1) = \mathbb P(X^{(1)} = x^{(1)}| Y = 1)\times \mathbb P( X^{(2)} = x^{(2)} | Y = 1). $$ Pour estimer chacun des deux termes du produit, on peut utiliser la loi des grands nombres comme précedemment. Par exemple, $\mathbb P(X^{(1)} = x^{(1)}| Y = 1)$ peut être approché par $\frac{N^{(1)}_1(n)}{M_1(n)}$, où $N^{(1)}_1(n)$ est le nombre de fois où on a observé la caractéristique $x^{(1)}$ et l’état du trafic $1$ parmi les données d’entraînement (par exemple le nombre de fois où la circulation était impossible sur le Mail François Mitterand), et $M_1(n)$ est le nombre de fois où on a observé l’état du trafic $1$ parmi les données d’entraînement (c’est-à-dire le nombre de fois où on a observé que la circulation était impossible). Cela permet de séparer les caractéristiques en entrée, au prix d’une hypothèse forte d’indépendance.
Quelques références
https://fr.wikipedia.org/wiki/Classification_na%C3%AFve_bay%C3%A9sienne